อะไรคือ P, NP, NP-Complete และ NP-Hard
สำหรับคนที่ศึกษา Theory Computer Science อาจจะได้เคยเห็นคนพูดถึงว่าปัญหานี้เป็น P และปัญหานี้เป็น NP มันคืออะไรกันแน่
Quick recap เผื่อลืมว่าแต่ละ Big O time complexity ใช้ running time เท่าไร เรียงจากใช้เวลาน้อยสุด ไปใช้เวลาเยอะสุด
\(O(1)\) => constant-time
\(O(\log_2(n))\) => logarithmic - time
\(O(n)\) => linear-time
\(O(n^2)\) => quadratic-time
\(O(n^k)\) => polynomial-time
\(O(k^n)\) => exponential-time
\(O(n!)\) => factorial-time
โดยที่ \(k\) เป็น constant และ \(n\) เป็นจำนวน input
สมมุติว่าเราเป็น researcher ที่มีเป้าหมายในการหา algorithm ที่สามารถแก้ปัญหาได้เร็วขึ้น
เช่นเรารู้ว่าการค้นหาของใน array สามารถหาคำตอบได้ใน polynomial time หรือ \(O(log(n))\) แต่เราต้องการ algorithm ที่ทำการค้นหาได้ใน constant time เช่น \(O(1)\)
หรือเรารู้ว่าปัญหาอย่าง traveling salesman สามารถหาคำตอบได้ใน exponential time \(O(2^n)\) แต่เราต้องการแก้ปัญหาในได้ใน polynomial time
แต่เรายังไม่รู้คำตอบว่าจะเขียน algorithm นี้ยังไง ใน polynomial time สิ่งที่เราพยายามทำได้ก่อนก็คือแสดงว่ามันมีคำตอบนะโดย
- เราจะพยายามแสดงว่าปัญหาใน time complexity นั้นๆ มันเกี่ยวข้องกัน เช่นปัญหา knapsack สามารถแปลงไปเป็นปัญหา traveling salesman ได้ ถ้าเราสามารถแก้ได้อันใดอันหนึ่งก็ถือว่ามันมีคำตอบ
- ถ้าเราไม่สามารถเขียน algorithm แบบ deterministic ได้ เราก็เขียน algorithm แบบ non-deterministic บางส่วนไปก่อน
Deterministic Algorithm
deterministic คือ algorithm ที่เวลาเราใส่ input ตัวหนึ่ง ไม่ว่ากี่รอบมันก็จะออกมาเหมือนเดิม ส่วน non-deterministic ก็คือตรงกันข้าม
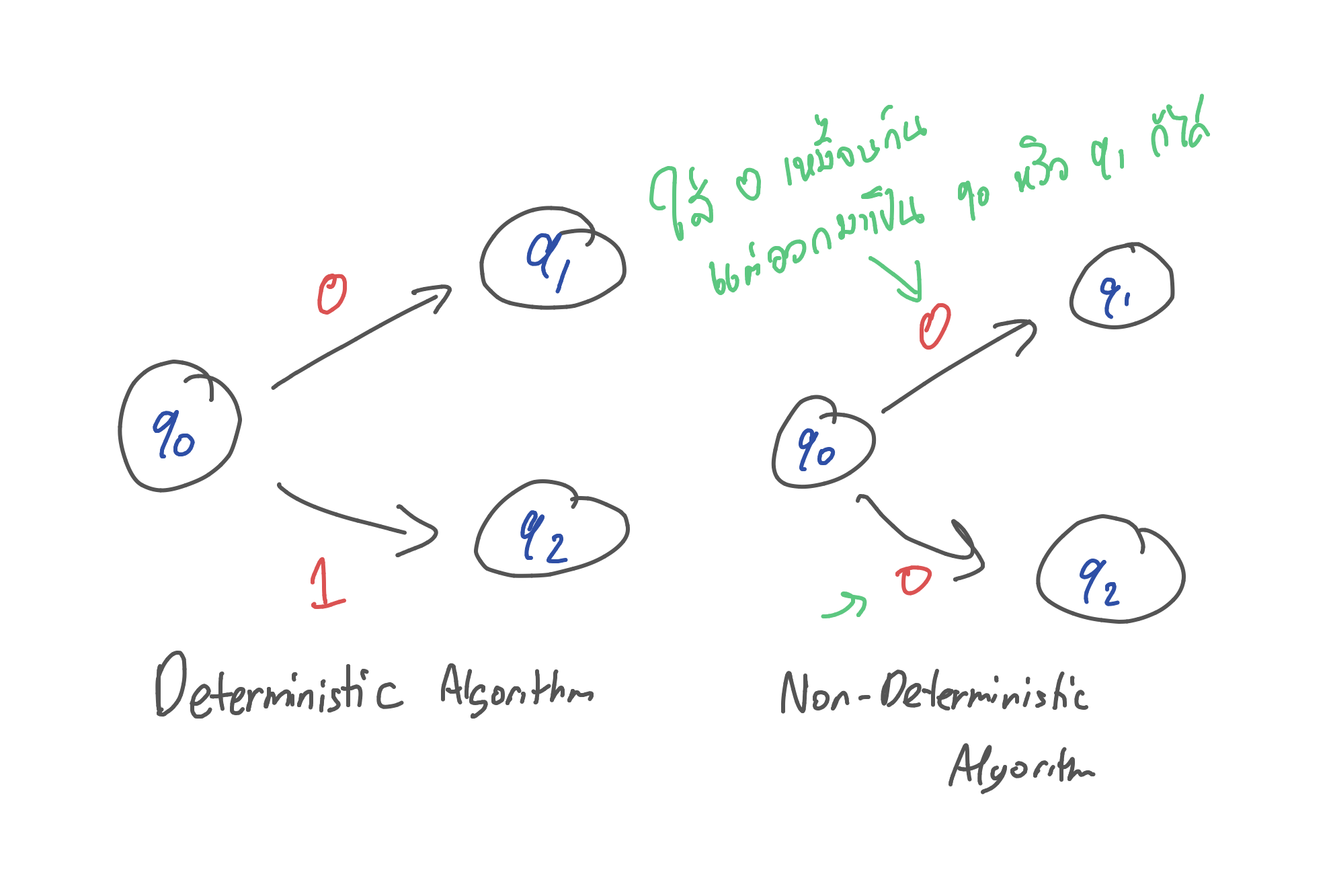
โดยที่เราสามารถเขียน non-deterministic search algorithm ที่เป็น constant time ได้ดังนี้
function search(A, key) {
j = choice(a) // คิดซะว่าเป็น constant O(1)
if (A[j] == key) then
{
write(j);
success(); // คิดซะว่าเป็น constant O(1)
}
write(0);
failure(); // คิดซะว่าเป็น constant O(1)
}
โดยที่เรายังไม่รู้ว่า choice() นั้นทำงานยังไง แต่เรา assume ว่ามันทำงานได้ และใช้เวลาแค่ \(O(1)\) ในอนาคตอาจจะมีคนมาแก้ปัญหา choice() นี้แทนเราได้
P = Deterministic polynomial time
P หรือ Polynomial time คือ
ปัญหานั้นต้องสามารถแก้ได้ในเวลา \(O(C * n^k)\) โดยที่ \(C > 0\), \(k > 0\), \(C\) และ \(k\) เป็น constant และ \(n\) เป็นจำนวน input โดยที่ค่า \(k\) ควรจะน้อยกว่า \(n\) ไม่งั้น algorithm จะคล้าย exponential มากกว่า
เราอยากได้ algorithm ที่อยู่ในกลุ่มนี้เพราะว่าเราสามารถให้ computer ณ ปัจจุบันที่เป็น Deterministic Turing Machine แก้ปัญหาได้เสร็จในระยะเวลาที่ไม่นานเกินไป
NP = Non-deterministic Polynomial Time
NP คือปัญหาที่ไม่สามารถแก้ได้โดยภายใน Polynomial Time แต่สามารถเช็คคำตอบได้ใน Polynomial Time โดยเป็นปัญหาที่ใช้เวลาแก้เป็น exponential เช่นปัญหาที่มี Time Complexity เป็น \(O(n^n)\), หรือ \(O(2^n)\)
เช่นปัญหา Integer Factorization หรือการแยกตัวประกอบ ที่มี Complexity เป็น \(O(k^n)\) แต่เราสามารถเช็คได้ใน polynomial time เพียงแค่คูณมันกลับเข้าไป
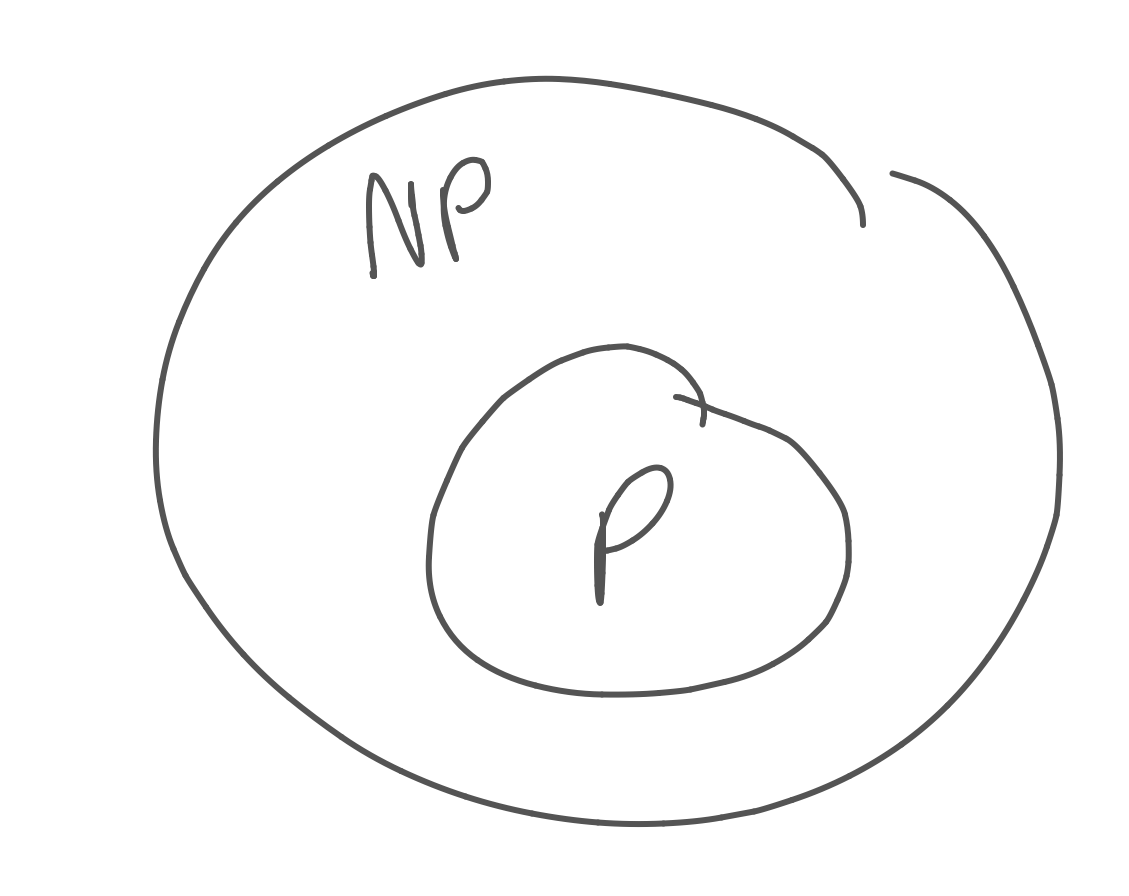
ภาพนี้ที่เป็นภาพที่เราจะเห็นค่อนข้างบ่อย ซึ่งแปลว่าปัญหาที่เป็น P เป็น subset ของ NP และเคยเป็น NP มาก่อน
เช่นก่อนหน้าที่จะมี merge sort เราไม่รู้ว่าจะแก้ปัญหานี้ยังไงใน polynomial time แต่เราสามารถเขียนให้มันเป็น non-deterministic polynomial time ได้ พอเราค้นพบ algorithm merge sort ปัญหาที่เคยเป็น NP ก็กลายเป็น P
NP-Complete
ข้อแตกต่างระหว่าง NP และ NP-Complete คือสิ่งที่เรียกว่า completeness
ความหมายของมันคือ \(Y\) เป็น NP-Complete ถ้าเราสามารถแปลง NP Problem \(X\) ไปเป็น \(Y\) ได้โดยใช้ polynomial time
ซึ่งหมายความว่าถ้าสามารถแก้ NP-Complete อันใดสักอันหนึ่งได้ใน polynomial time ได้ อีกอันหนึ่งก็สามารถแก้ได้เช่นเดียวกัน
วิธีการแสดงว่า \(X\) สามารถเป็น \(Y\) ได้เรียกว่าการทำ Reduction
ใน research Reducibility Among Combinatorial Problems ของ Karp ได้ prove 21 algorithms ว่าสามารถ reduce ไปมาได้ และแสดงให้เห็นว่าพวกมันเหล่านั้นเป็น NP-Complete ยกตัวอย่างเช่นปัญหา Satisfiability, Traveling Salesman, และ Knapsack
NP-Hard
สุดท้าย ปัญหาที่ยากที่สุดใน Computer science ที่ไม่แค่แก้ไขปัญหายาก ยังไม่รู้ด้วยซ้ำว่าจะตอบคำถามยังไง ซึ่งมีความยากอย่างน้อยเท่ากับ NP แต่อาจจะยากยิ่งกว่า
ความหมายของ NP-Hard คือ ปัญหา \(Y\) เป็น NP-Hard ถ้าเราสามารถแปลง NP-Complete \(X\) เป็น \(Y\) ได้ใน polynomial time
สิ่งที่ผมไม่ได้บอกก่อนหน้านี้ก็คือ P, NP, NP-Complete คือปัญหาที่เป็น Decision Problem หรือ ปัญหาที่เราสามารถตอบได้ว่ามันถูก หรือไม่ถูก แต่ NP-Hard ไม่จำเป็นต้องเป็น Decision problem
แต่ก็ยังมีปัญหาที่เป็น NP-Hard ที่เป็น decision แต่ไม่ใช่ NP เช่น halting problem อีกด้วย เพราะฉะนั้น NP-hard problem ไม่จำเป็นต้องเป็น NP
หน้าตา Diagram P, NP, NP-Complete และ NP-Hard
สุดท้ายเราก็จะได้ diagram ตัวนี้ที่เราเคยเห็นค่อนข้างบ่อย
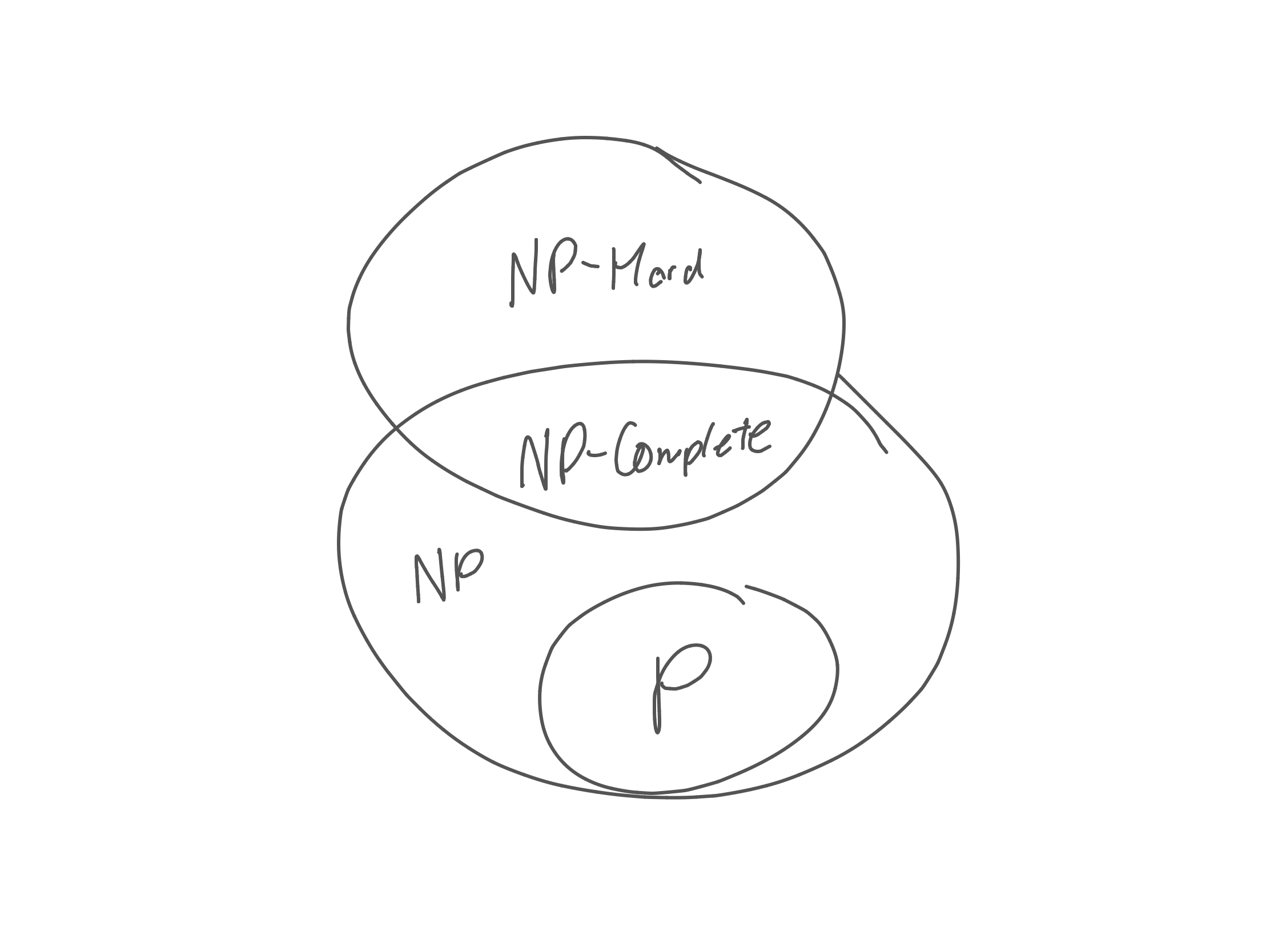
ซึ่งที่เราอธิบายและทำความเข้ามาทั้งหมดอยู่บนพื้นฐานว่า P != NP แต่ปัญหาคือเรายัง prove มันไม่ได้ ถ้าเกิด P = NP จริง แปลว่าปัญหาที่เป็น NP และ NP-Complete จะสามารถแก้ได้ใน polynomial time มีรางวัลให้สำหรับคนที่สามารถ prove ได้ว่า P != NP ด้วยนะครับ Millennium Prize Problems - Wikipedia
ถ้าเกิด P = NP จริง จะทำให้หลาย encryption และ cryptography algorithm พัง เพราะตอนนี้หลาย algorithm ที่เกี่ยวกับ security ทั้งหลายแหล่ assume ว่าการโจมตี algorithm นั้นๆใช้เวลานานเกินกว่าจะเป็นไปได้จริง